In this vignette, we show how to detect the presence of random responses using the uniformity test. This test is based on the idea that given respondent-level item order randomization, recorded responses will follow a uniform distribution in the absence of random responses. The uniformity test can be easily implemented even when researchers do not have any anchor ranking questions.
Recorded Responses
In an earlier vignette, we showed how to perform bias correction on ranking questions using the anchor question. But how do we know if there is a need for bias correction in the first place?
The distribution of rankings of recorded responses can show whether there are indeed random responses. Before we demonstrate this, first, we must clarify: what are recorded responses? The following figure shows the difference between observed ranking and recorded response, given item order randomization.
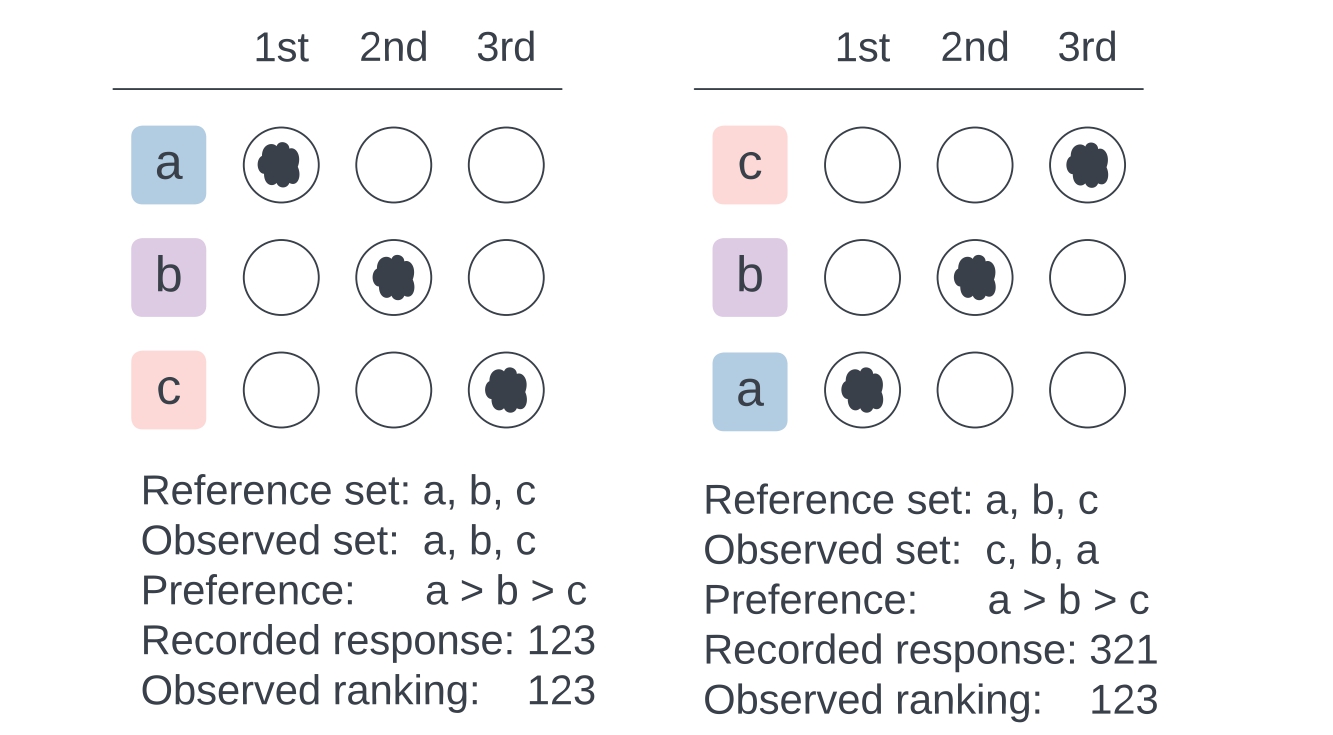
Suppose that we prefer items a-b-c in that order. And in the ranking exercise, they were presented in the order of a-b-c. Then, given the ordered reference set a-b-c, my observed ranking and recorded response are both 1-2-3. Recorded responses are identical to observed rankings when item orders are fixed. However, when an item order is not fixed, the observed choice set differs across respondents.
If, for example, the items were presented in the order of c-b-a, then our observed ranking is 1-2-3, while our recorded response is 3-2-1. This is because the observed ranking is the ranking of the items in the order of the reference set, regardless of the order in which they were presented. On the other hand, the recorded response is the ranking of the items in the order in which they were presented.
Recovering Recorded Responses
The function recover_recorded_responses recovers the
recorded responses from the observed rankings and the item order
randomization. The function takes the true_order,
presented_order, and df for data frame as
arguments.
For example, in identity, the app_identity
column contains the observed rankings, and the
app_identity_row_rnd column contains the how the items were
presented via item order randomization. Thus the presented order is
app_identity_row_rnd and the true order is
app_identity.
For the first respondent, with the reference choice set of {party, religion, gender, race}, this respondent ranked party-gender-race-religion (1-4-2-3, i.e., party is first place, religion is fourth place, gender is second place, and race is third place). However, the items were presented to the respondent in the order of religion-party-race-gender (2-1-4-3). Thus, the recorded response is 4-1-3-2 (first option shown was religion, thus fourth place, second option shown was party, thus first place, the third option shown was race, thus third place, and the fourth and last option shown was gender, thus second place). It’s a bit tricky at first, so please read this explanation carefully!
recover_recorded_responses(
presented_order = "app_identity_row_rnd",
true_order = "app_identity",
df = head(identity[, c("app_identity", "app_identity_row_rnd")], 10)
)
#> # A tibble: 10 × 3
#> app_identity app_identity_row_rnd app_identity_recorded
#> <chr> <chr> <chr>
#> 1 1423 2143 4132
#> 2 1423 1324 1243
#> 3 3412 2134 4312
#> 4 1423 3421 2341
#> 5 4132 2134 1432
#> 6 3124 4123 4312
#> 7 1234 3124 3124
#> 8 4312 1234 4312
#> 9 3124 4132 4321
#> 10 4321 1432 4123
## Alternatively, for the first respondent
recover_recorded_responses(
presented_order = "2143",
true_order = "1423",
)
#> [1] "4132"Uniformity Test
Theory
In Atsusaka and Kim (2024), we prove that once there is item order randomization, the recorded responses will follow a uniform distribution in the absence of random responses. Suppose, for example, that everyone prefers a-b-c in that order. Some respondents will have a recorded response of 1-2-3, while others will have 3-2-1, given the differently observed sets of items. Then, in the absence of random responses, the proportion of recorded responses for each possible ranking should converge to 1/24 = 0.0417, given that there are 4! = 24 possible ways to rank the items. Accordingly, a notable deviation from the uniform distribution provides evidence for the presence of random responses.
What happens with random responses? The figure below shows some likely scenarios.
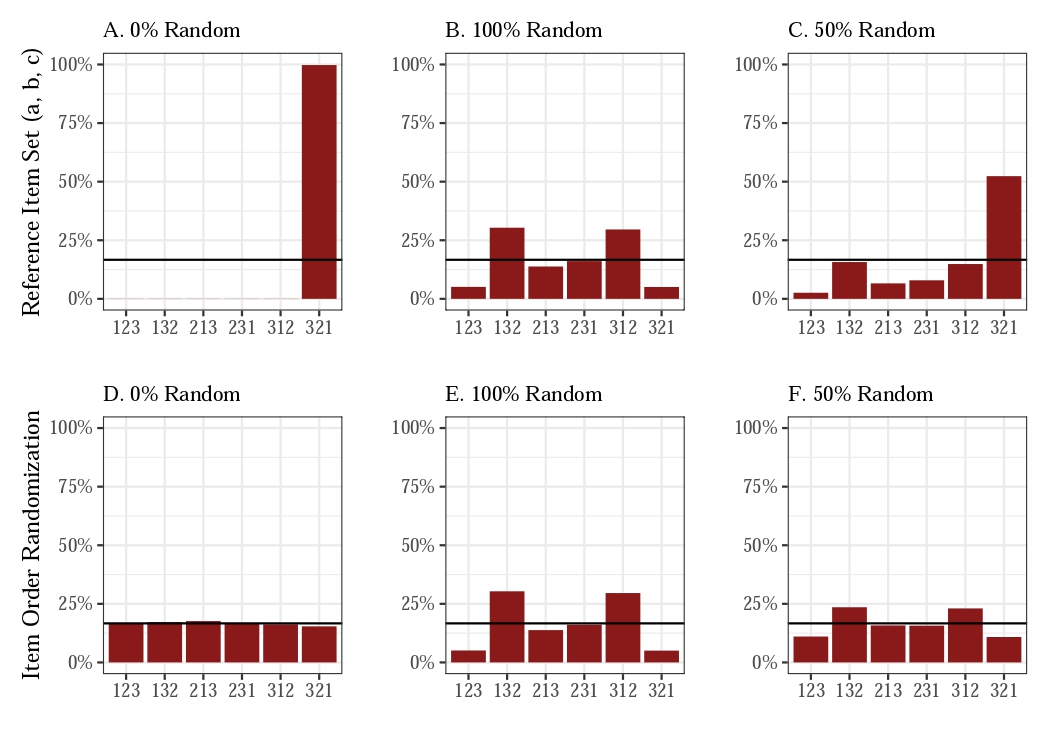
In this hypothetical world, suppose everyone prefers items in the order of c-b-a. With a reference item set of (a, b, c), the recorded responses will always be 3-2-1 (panel A). If item order is randomized, recorded responses will be uniformly distributed (panel D).
Now suppose that random responses occur in patterns such as panels B and E. If 50% of responses are random, recorded responses will be like panel C if the reference set is fixed for all respondents, or like panel F if the reference set is randomized.
Test
The uniformity test checks whether the recorded responses follow a uniform distribution. Non-uniformity in the test suggests the presence of random responses.
uniformity_test(identity, "app_identity")
#>
#> Chi-squared test for given probabilities
#>
#> data: tab
#> X-squared = 765.6, df = 23, p-value < 2.2e-16The results indicate that the recorded responses are not uniformly distributed, suggesting random responses in the main identity ranking question. The uniformity test was also applied to detect ballot order effects in ranked-choice voting (e.g., Atsusaka (2024)).
Validity of the Anchor Question
Checking for uniformity also validates the usage of the anchor question. Although the assumption in the paper is simply that the proportion of random responses is the same in the main and the anchor question, the more implicit assumption is that those who are answering the anchor question correctly are not providing random responses to the anchor question.
We can check this by comparing the recorded responses of those who answered the anchor question correctly and incorrectly.
## Correctly answered the anchor question
tab <- table(identity$anc_identity_recorded[identity$anc_correct_identity == 1])
round(prop.table(tab) * 100, digits = 1)
#>
#> 1234 1243 1324 1342 1423 1432 2134 2143 2314 2341 2413 2431 3124 3142 3214 3241
#> 6.5 3.8 3.1 4.2 5.0 4.2 3.1 2.8 3.6 3.3 5.2 4.1 3.8 4.2 5.6 3.2
#> 3412 3421 4123 4132 4213 4231 4312 4321
#> 4.5 4.4 3.4 4.8 4.0 4.5 4.8 3.8
uniformity_test(tab)
#>
#> Chi-squared test for given probabilities
#>
#> data: data
#> X-squared = 31.698, df = 23, p-value = 0.1066
## Incorrectly answered the anchor question
tab <- table(identity$anc_identity_recorded[identity$anc_correct_identity == 0])
round(prop.table(tab) * 100, digits = 1)
#>
#> 1234 1243 1324 1342 1423 1432 2134 2143 2314 2341 2413 2431 3124 3142 3214 3241
#> 13.1 6.4 2.7 2.4 4.3 4.9 7.0 4.6 5.2 3.7 2.4 2.7 3.0 2.1 2.4 3.0
#> 3412 3421 4123 4132 4213 4231 4312 4321
#> 0.9 3.7 4.0 2.7 3.0 4.6 4.0 7.0
uniformity_test(tab)
#>
#> Chi-squared test for given probabilities
#>
#> data: data
#> X-squared = 107.95, df = 23, p-value = 5.793e-13As can be seen, while there is insufficient evidence to reject the null hypothesis for those who answered the anchor question correctly, the recorded responses of those who answered the anchor question incorrectly offer clear evidence for non-uniformity, where about 20% of respondents submitted either 1234 or 4321.
Caveat: Augment Missing Permutation Patterns
One thing to note: in a small sample size, some ranking patterns
might not be realized. For example, in a sample of 10 respondents, it is
possible that the pattern 1234 is not observed. In such cases, it is
important to augment the missing permutation patterns with a count of 0,
which can be done with permn_augment.
tab <- table(head(identity$app_identity_recorded))
tab ## only five patterns out of twenty-four possible patterns
#>
#> 1243 1432 2341 4132 4312
#> 1 1 1 1 2
permn_augment(tab)
#> 1234 1243 1324 1342 1423 1432 2134 2143 2314 2341 2413 2431 3124 3142 3214 3241
#> 0 1 0 0 0 1 0 0 0 1 0 0 0 0 0 0
#> 3412 3421 4123 4132 4213 4231 4312 4321
#> 0 0 0 1 0 0 2 0Within , the function is already called.
